반응형
μoperation의 4가지 종류
1. register-transfer
2. arithmetic
3. logic
4. shift μoperations
| Symbolic designation |
Description |
| R3 <- R1 + R2 | R1 + R2의 정보가 R3로 전달된다. |
| R3 <- R1 - R2 | R1 - R2의 정보가 R3로 전달된다. |
| R2 <- R2 | R2 정보의 보수를 나타낸다.(1's complement) |
| R2 <- R2 + 1 | R2의 2의 보수를 나타낸다. |
| R3 <- R1 + R2 + 1 | R1 + R2의 2의보수 (빼기를 진행) |
| R1 <- R1 +1 | R1의 정보에 1증가시킨다. |
| R1 <- R1 - 1 | R1의 정보에 1감소시킨다. |
Binary Adder
n-bit binary adder는 n개의 full-adders를 필요로한다.

위의 그림은 4-bit binary adder이다.
4개의 full-adder를 가지고 있으며 full-adder는 입력 3개에 출력 2개를 가진다.
Binary Adder-Subtractor (woth M contorl signal)
위의 제목에서 M은 Minus를 뜻한다.
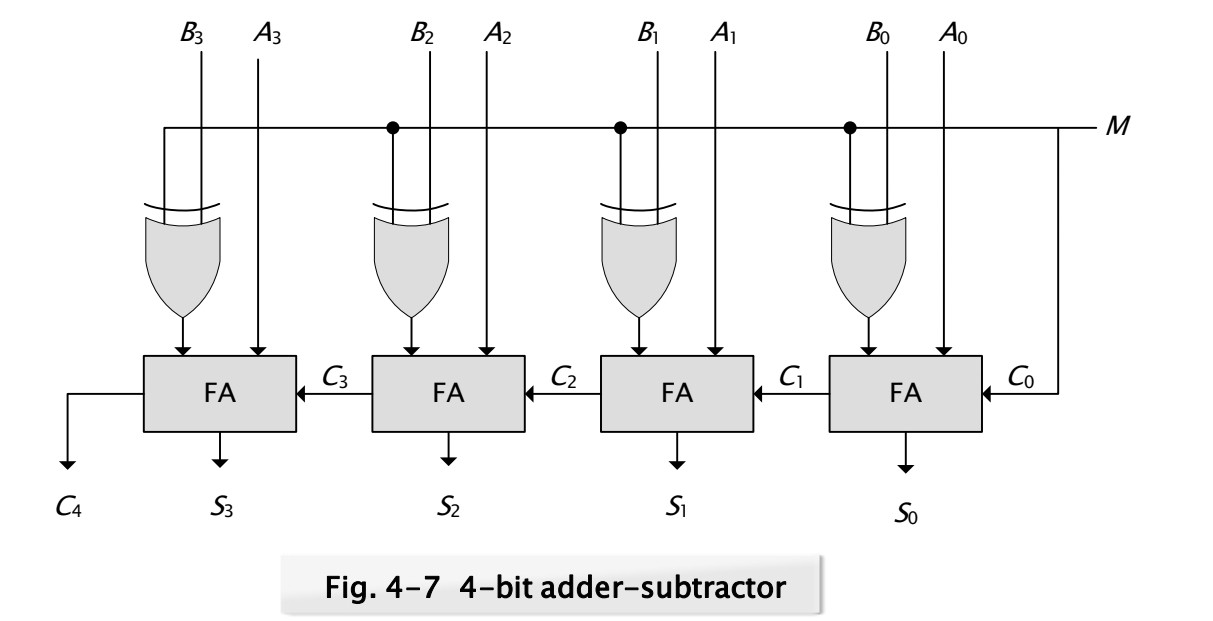
위의 그림은 binary adder-subtractor를 나타낸다.
4개의 Full adder와 4개의 XOR gate를 가진다.
이제 4-7 그림의 작동원리를 알아보자
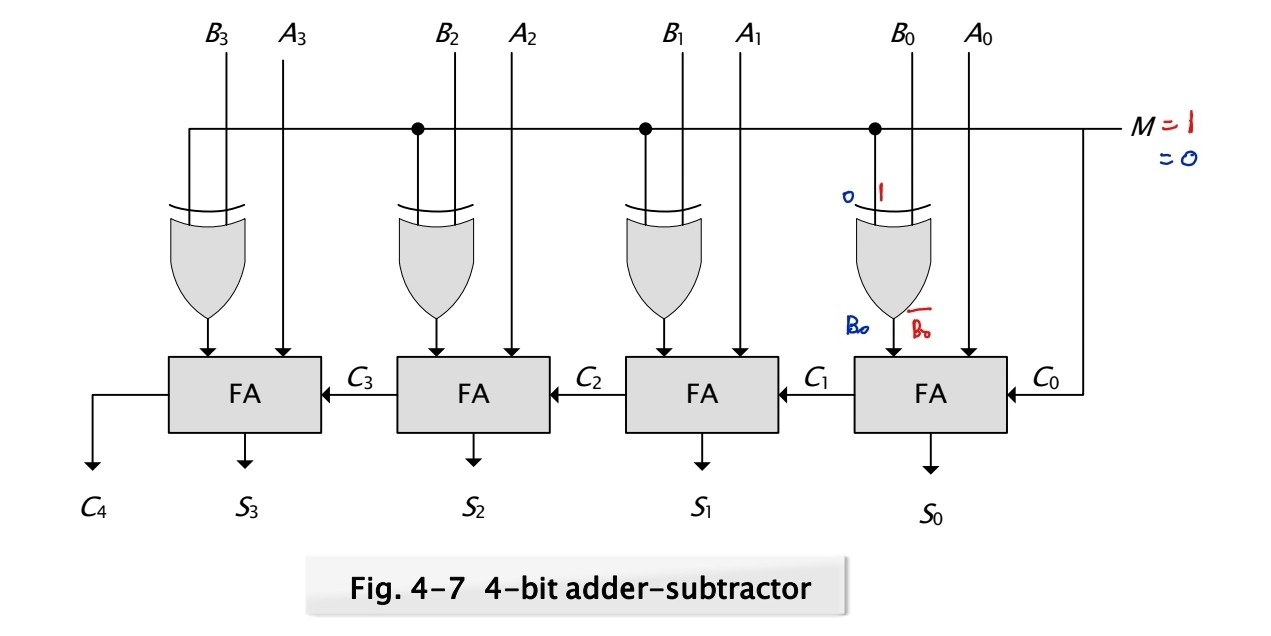
1. if M = 0, B ⊕ 0 = B and C0 = 0 <=> S = A + B(addition)
2. if M = 1, B ⊕ 1 = B and C0 = 0 <=> S = A +(B - 1) (addition)
작동원리에 대한 것은 그림을 보고 이해해보자
Binary Incrementer
Register 값에 1을 더하는 μoperation은 아래와 같다.

A의 비트가 1101일 때 binary incrementer는 다음과 같다.

위의 그림의 결과에 따라 1110이 나오는 것을 알 수 있다.
Arithmetic Circuit
다음은 산술회로를 보자
결과 부터 말하면 D = A + Y + Cin이 된다.
Arithmetic circuit function table

4-bit arithmetic circuit
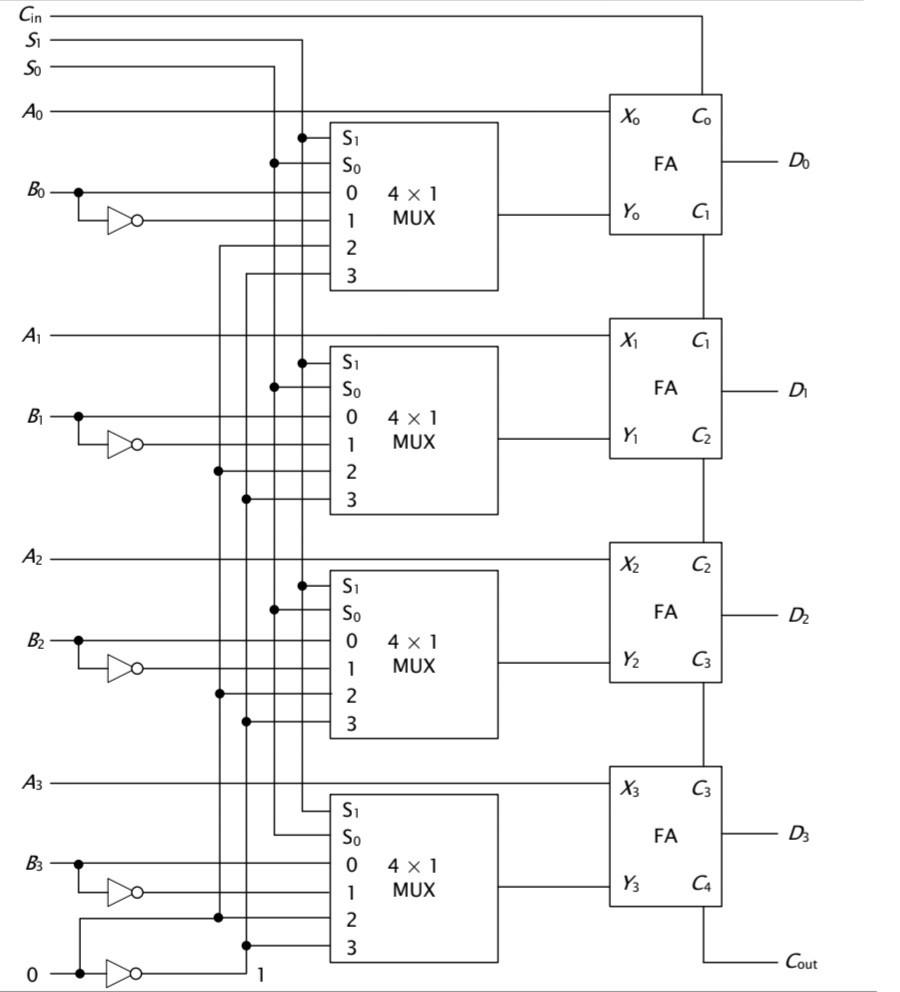
위의 산술 회로 함수 테이블 가지고 4-bit 산술 회로를 해보자
예시로는 S1 = 0, S0 = 1, Cin= 1인 빼기 마이크로연산을 해보겠다.
4-bit A = 1011, B = 0110이라고 가정하자

위의 예시를 진행하였을 때 D = 0101이 나온다.
반응형
'컴퓨터구조' 카테고리의 다른 글
| [컴퓨터구조] 기본 컴퓨터 조직 및 디자인(Basic Computer Organization and Design), 컴퓨터 레지스터(Comput (0) | 2023.09.25 |
|---|---|
| [컴퓨터구조] 논리 마이크로연산(Logic Microoperations), 쉬프트 마이크로연산(Shift Microoperations) (0) | 2023.09.19 |
| [컴퓨터 구조] 레지스터 전송(Register Transfer) (0) | 2023.09.11 |
| [컴퓨터구조] Error Detection Codes 패리티 비트(Parity bit)에 대해 (0) | 2023.09.11 |
| [컴퓨터구조] Data Representation(데이터 표현) (0) | 2023.09.07 |




댓글