[시스템프로그래밍] 3장 실수의 표현 및 처리
1장 복습(Computer System)
https://youknow301.tistory.com/106
2장 복습(정수의 표현)
https://youknow301.tistory.com/111
소수점 숫자 표시 방법
1. 고정 소수점 방식
- 숫자에서 소수점의 위치를 고정시켜서 숫자를 표현한다.
- ex) 1234.6666
- 가장 큰 수는 9999.9999가 되며 가장 작은 수는 0000.0001이 된다.
2. 부동 소수점 방식
- 소수점의 위치가 정해지지 않는다.
- 유효숫자 x 소수점의 위치 형태로 표시한다.
- ex) 8자리 유효숫자와 2자리 지수로 표현한다면
가장 큰 수 : 9.9999999E+50
가장 작은 수 : 0.0000001 E-49가 된다.
IEEE Floating Point
IEEE 표준 754
전기전자공학자협회(IEEE - "아이 트리플 이"라고 읽는다)는 모든 전자 및 컴퓨터 기술을 총망라하는 전문 소사이어티이다.
현재 모든 주요 CPU에서 IEEE Floating Point라는 이름으로 지원이 된다.
장점
수치해석적인 측면을 고려하여 정의가 되었다.
-> rounding, overflow, underflow 등에 유용하다.
단점
빠른 연산을 수행하기가 어려운 단점이 있다.
2진 소수
2진 소수는 다음과 같은 식으로 나타낼 수 있다.
예제
5.75를 이진 소수로 나타내보면 다음과 같다.
여기서 우측으로 쉬프트 해보면 다음과 같은 결과가 나온다.
5.75를 좌측으로 쉬프트 해보면 다음과 같은 결과가 나온다.
결론
우측으로 쉬프트 하면 2를 나눈 효과가 나온다.
좌측으로 쉬프트 하면 2를 곱한 효과가 나온다.
2진 소수의 단점
2진 소수의 경우 다음과 같은 형태의 소수들만 정확한 표시가 가능하다.
하지만 소수점 이하의 비트들이 무한 반복되는 경우는 정확히 표시할 수 없다.
무한 반복되는 소수점을 표현하기 위해 등장한 것이
IEEE Floating Point 방법이다.
IEEE Floating Pint 표준
소수의 표현 방법
아래의 형태와 같은 모습으로 소수를 표시한 후에 S, M, E를 인코딩해서 저장한다.
부호비트 s는 양수/음수 여부를 표시한다.
유효숫자 M 은 [1.0, 2.0) 또는 [0.0, 1.0) 사이의 실수 값을 표시한다.
지수 E는 2의 지수 제곱을 표시한다.
인코딩 방법
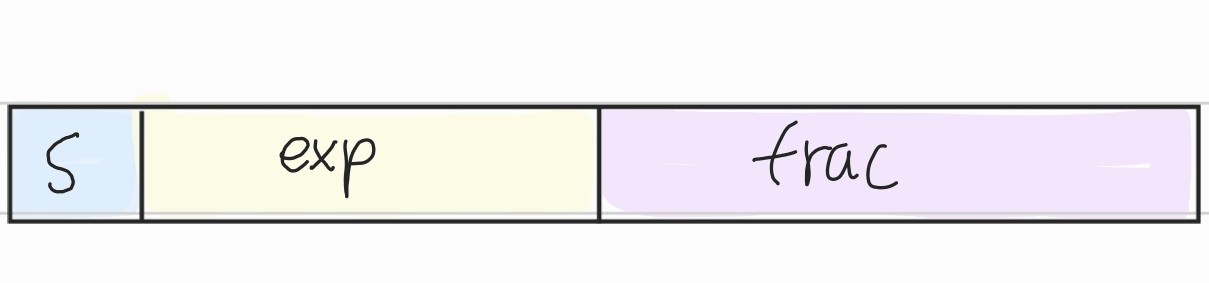
필드의 정의
MSB는 부호 비트이다.
exp 필드는 E 부분을 인코딩한 것이다.
frac 필드는 M 부분을 인코딩한 것이다.
exp필드에 따른 구분
exp가 어떠한 숫자가 오느냐에 따라 1. 정규화된 값(Normalized values), 2. 비정규화 값(Denormalized values), 3. 특수값(Special values)이 온다.
1. 정규화된 값(Normalized values)
정규화된 값의 경우 exp ≠ 00000000, exp ≠11111111 이 두 개를 제외한 나머지가 된다.
지수(E)의 경우 조정된 값(biased value)의 형식을 따른다.
E = exp - bias, exp = E+ bias가 된다.
exp : unsigned value
bias : 조정된 Bias value
bias =
여기서 e는 지수비트이다.
유효숫자(M)의 경우 1로 시작하는 것으로 간주한다.
2. 비정규화된 값(Denormalized values)
비정규화된 값의 경우 exp = 00000000의 경우 해당이 된다.
인코딩 방법
E = 1 - Bias
비정규화 인코딩의 사용 -> 2가지로 나뉜다.
1. exp = 000... 0, frac = 000... 0
-> 0을 표시한다.
-> +0와 -0이 다름 주의!
2. exp = 000... 0, frac ≠ 000...0
-> 0.0에 매우 근접한 소수값을 표시
3. 특수값(Special values)
특수값의 경우 exp = 11111111
두 가지 경우에 사용한다.
1. exp =111...1, frac = 000...0
->무한대 ∞를 표시
2. epx = 111...1, frac ≠ 000...0
-> Non -a - Number (NaN)
지수값 표시
| Exp | exp | E | |
| 0 | 0000 | -6 | 1/64 |
| 1 | 0001 | -6 | 1/64 |
| 2 | 0010 | -5 | 1/32 |
| 3 | 0011 | -4 | 1/16 |
| 4 | 0100 | -3 | 1/8 |
| 5 | 0101 | -2 | 1/4 |
| 6 | 0110 | -1 | 1/2 |
| 7 | 0111 | 0 | 1 |
| 8 | 1000 | 1 | 2 |
| 9 | 1001 | 2 | 4 |
| 10 | 1010 | 3 | 8 |
| 11 | 1011 | 4 | 16 |
| 12 | 1100 | 5 | 32 |
| 13 | 1101 | 6 | 64 |
| 14 | 1110 | 7 | 128 |
| 15 | 1111 | n/a | (inf,NaN) |
노란색 부분 -> 비정규화
나머지 -> 정규화